O que são diagonais dos polígonos?

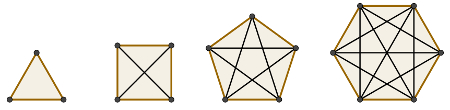
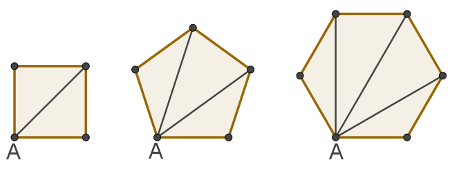
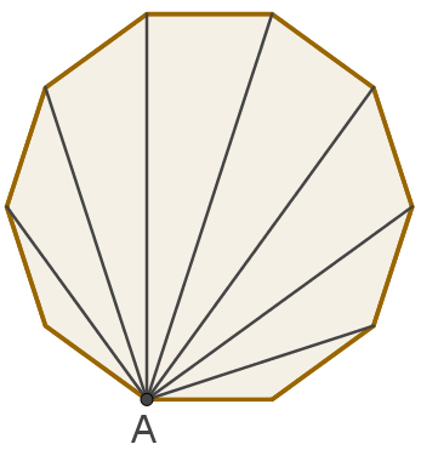
Os polígonos são figuras geométricas bidimensionais formadas por segmentos de reta. Entre os elementos dos polígonos, estão os vértices, lados e diagonais. As diagonais de um polígono são segmentos de reta que ligam dois de seus vértices não consecutivos. As imagens a seguir mostram as diagonais de alguns polígonos em preto:

Observe que o número de diagonais aumenta quando aumentamos também o número de lados do polígono. O triângulo possui zero diagonais, o quadrado, duas, o pentágono, cinco, e o hexágono, nove.

Encontrar uma relação entre o número de diagonais de um polígono e seu número de lados não é tarefa fácil, já que ela parece não existir. No entanto, essa relação existe e depende do número de diagonais que partem de um único vértice do polígono.

Diagonais que partem de um único vértice

Na imagem a seguir, veja a quantidade de diagonais que partem do vértice A dos polígonos em destaque:

Do quadrado, parte uma diagonal do vértice A. Do pentágono, duas, e do hexágono, três diagonais. A imagem a seguir mostra as diagonais que partem do vértice A de um decágono.

Observe que essa figura geométrica possui dez lados e de cada vértice partem sete diagonais. Veja abaixo uma tabela que relaciona o número de lados da figura e o número de diagonais partindo de um mesmo vértice (d_v):

Note que o número de diagonais partindo de um mesmo vértice é sempre igual ao número de lados do polígono menos três unidades. Assim, se o lado do polígono for representado pela letra n, teremos:

d_v = n – 3

Número total de diagonais de um polígono

O número total de diagonais (d) do polígono pode ser obtido a partir da seguinte expressão:

d = n(n – 3)
     2

Em outras palavras, o número de diagonais de um polígono sempre é o produto entre o número de lados e o número de diagonais que partem do mesmo vértice dividido por dois. Essa relação vale para todo polígono convexo, ou seja, que não possui reentrâncias.

Exemplos

1º Exemplo – Qual o número de diagonais de um polígono que possui 40 lados? Quantas diagonais partem de cada vértice desse polígono?

Solução: Não é necessário desenhar a figura para responder a questões como essas. Para encontrar o resultado da primeira pergunta, faça:

d = n(n – 3)
      2

d = 40(40 – 3)
      2

d = 40(37)
     2

d = 1480
      2

d = 740

A partir do mesmo vértice:

d_v = n – 3

d_v = 40 – 3

d_v = 37

Portanto, são 740 diagonais no total e 37 diagonais partindo do mesmo vértice.

2º Exemplo – Qual o número de lados de um polígono que possui 25 diagonais partindo de cada vértice?

Solução:

d_v = n – 3

25 = n – 3

n = 25 + 3

n = 28

São 28 lados.

Por Luiz Paulo Moreira
Graduado em Matemática