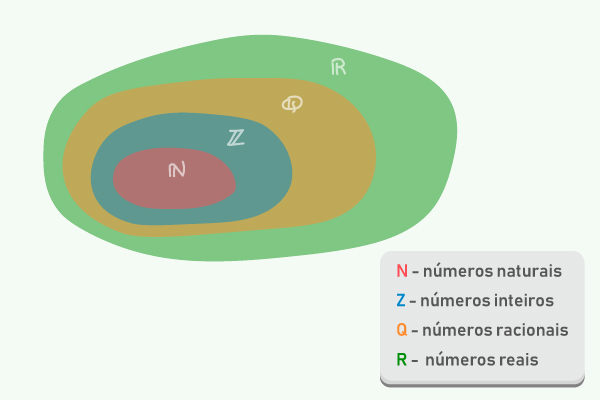
O que são conjuntos numéricos?
Os conjuntos numéricos são uma maneira de classificar os números de acordo com as suas características. São eles: números naturais, inteiros, racionais, irracionais e reais.

Escrito por: Raul Rodrigues de Oliveira
Graduado em Matemática pela Universidade Federal de Goiás. Atua como professor do programa PIC Jr. (OBMEP) e como professor preceptor do programa Residência Pedagógica. Também é professor concursado da Seduc-GO, gestor escolar e produtor de conteúdo didático.
Deseja fazer uma citação?
OLIVEIRA, Raul Rodrigues de.
"O que são conjuntos numéricos?"; Brasil Escola.
Disponível em: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-conjuntos-numericos.htm. Acesso em 03 de
fevereiro
de 2026.
Copiar
Artigos Relacionados
O que são equações incompletas do segundo grau?
O que são equações incompletas do segundo grau? Essas expressões podem ser escritas como ax2 + bx + c = 0, em que b = 0 ou c = 0, ou ambos são iguais a zero.O que são múltiplos?
Múltiplos de um número inteiro são o resultado da multiplicação desse número por todos os outros números inteiros.O que são números complexos?
O que são números complexos? Trata-se de um novo conjunto numérico que excede o conjunto dos números reais.O que são números pares e ímpares?
O que são números pares e ímpares? Os pares são aqueles terminados em 0, 2, 4, 6 ou 8. Já os ímpares são aqueles que não são pares e são terminados em 1, 3, 5, 7 ou 9.O que são números racionais?
O que são números racionais? São elementos de um conjunto numérico formado por todos os números que podem ser escritos na forma de fração.O que são números reais?
O que são números reais? São números pertencentes a um conjunto numérico formado pela união de outros dois conjuntos: Racionais e Irracionais.O que é Conjunto dos Números Naturais?
O conjunto dos números naturais é o conjunto numérico mais simples e é formado pelos números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ...O que é MMC (mínimo múltiplo comum)?
O que é mínimo múltiplo comum (MMC)? Dados dois ou mais números, o MMC é o menor dos múltiplos que esses números possuem em comum.O que é domínio, contradomínio e imagem?
O que é domínio, contradomínio e imagem? Esses conjuntos numéricos estão presentes na definição e nos resultados obtidos em uma função.O que é fração?
O que é fração? É um modo de representar as partes pelas quais um objeto foi dividido. Assim, toda fração representa uma divisão e um número racional.Números racionais
Os números racionais podem ser representados em forma de fração, números decimais de finita ordem e dízimas periódicas.Números inteiros
O conjunto dos números inteiros é uma ampliação do conjunto dos números naturais, ou seja, agrupa os números naturais e os seus opostos, ou seja, os números negativos.Números irracionais
Números irracionais são todos aqueles números cuja representação decimal é uma dízima não periódica. São números irracionais as raízes não exatas, o π, entre outros.Conjuntos numéricos
Conjuntos numéricos possuem características específicas e são originados com base em determinadas operações.Cálculo Numérico
Conjunto dos números complexos
Notações Importantes sobre conjunto
Operações com conjuntos
Conjuntos são uma ideia que permeia vários campos da matemática desde seus primórdios. Nesse campo de estudo, temos algumas propriedades e importantes definições operatórias.Definição de Conjunto

Correção de redação Enem gratuita!
Corrigir agora!
Ferramentas
Cronograma de estudos
Jornada do Enem
Corrige Aqui
Conversor de números romanos
Tire Dúvidas
Calculadora SISU
Calculadora PROUNI
Jogo das Capitais
Palpites
Simulados Enem
Simulados Vestibulares