O que é círculo?
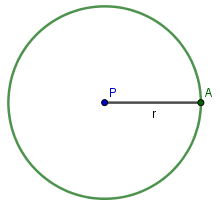
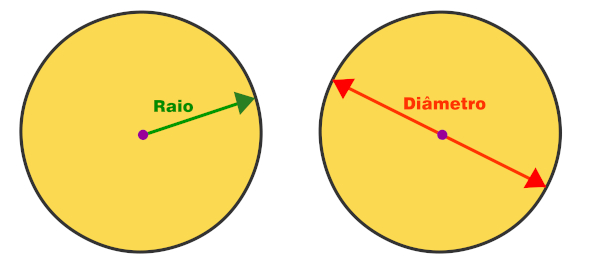
O círculo de centro P e raio r é o conjunto de pontos que estão a uma distância igual ou inferior a r de P. Círculo e circunferência são figuras geométricas distintas.

Escrito por: Maria Luiza Alves Rizzo
Autora, Leitora Crítica e Revisora de Matemática apaixonada por escrever. Especialista pela UFPI (2023) e Licenciada pela UFSM (2022), trabalha em projetos editoriais para o Ensino Fundamental, Ensino Médio e Pré-vestibular.
Deseja fazer uma citação?
RIZZO, Maria Luiza Alves.
"O que é círculo?"; Brasil Escola.
Disponível em: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-circulo.htm. Acesso em 03 de
fevereiro
de 2026.
Copiar
Artigos Relacionados
O que são as dimensões do espaço?
O que são as dimensões do espaço? São as possibilidades de obter as medidas de largura, comprimento e profundidade em figuras e sólidos geométricos.O que são monômios?
Monômios são expressões algébricas que têm um número, conhecido como coeficiente, multiplicando uma ou mais letras (variáveis), a parte literalO que são poliedros de Platão?
Os poliedros de Platão são aqueles que possuem características em comum, como é o caso do tetraedro, hexaedro, octaedro, dodecaedro e icosaedro.O que são posições relativas?
Para entender o que são posições relativas, deve-se saber que se relacionam com o número de interações entre duas figuras geométricas que ocupam o mesmo lugar no espaço.O que é circunferência?
O que é circunferência? Trata-se de conjuntos de pontos definidos a partir de um ponto fixo (centro) e uma distância (raio).O que é concavidade de uma parábola?
Para saber o que é concavidade de uma parábola, basta entender que essa figura representa uma função do segundo grau, em que o coeficiente a define a forma de sua reentrância.O que é círculo trigonométrico?
O que é círculo trigonométrico? Trata-se de um círculo em que todos os pontos estão relacionados com números reais e com ângulos.O que é função?
Uma função é uma relação matemática estabelecida entre duas variáveis. As funções podem ser injetoras, sobrejetoras, bijetoras e simples.O que é geometria?
O que é geometria? É o estudo das formas presentes na natureza e das propriedades que essas formas possuem.O que é gráfico?
O que é gráfico? É uma representação de informações obtidas em pesquisas por meio de formas geométricas para facilitar a leitura dos dados.Círculo e circunferência
A circunferência é uma região no plano formada por pontos que são equidistantes de um ponto fixo chamado centro. Círculo é a região interna dessa circunferência.Área do círculo
A área de um círculo de raio “r” é obtida pelo produto entre o número irracional pi (π) e o quadrado de “r”.
Correção de redação Enem gratuita!
Corrigir agora!
Ferramentas
Cronograma de estudos
Jornada do Enem
Corrige Aqui
Conversor de números romanos
Tire Dúvidas
Calculadora SISU
Calculadora PROUNI
Jogo das Capitais
Palpites
Simulados Enem
Simulados Vestibulares