As retas são elementos primitivos da geometria porque elas não podem ser definidas por outros conceitos mais básicos da geometria — uma reta é infinita e tem uma única dimensão. Normalmente uma reta é representada por uma letra minúscula do nosso alfabeto, por exemplo, reta r, reta s, reta t.
Quando comparamos a posição relativa entre duas retas, é possível realizar uma classificação das retas. Elas podem ser paralelas, quando não há nenhum ponto em comum, coincidentes, quando há infinitos pontos em comum, ou concorrentes, quando há um único ponto em comum.
Leia também: Ponto, reta, plano e espaço — conheça as noções primitivas da geometria
Tópicos deste artigo
- 1 - Resumo sobre retas
- 2 - O que são retas?
- 3 - Propriedades da reta
- 4 - Classificação das retas
- 5 - Tipos de retas
- 6 - Reta e semirreta
- 7 - Reta e segmento de reta
- 8 - Reta numérica e reta orientada
- 9 - Equação geral da reta
- 10 - Equação reduzida da reta
- 11 - Exercícios resolvidos sobre retas
Resumo sobre retas
- A reta é um elemento primitivo da geometria.
- A reta é infinita e tem apenas uma dimensão.
- Representamos as retas por letra minúscula do alfabeto, como reta r e reta s.
- Podemos classificar duas retas pela posição relativa entre elas.
- Paralelas: não têm pontos em comum.
- Coincidentes: têm infinitos pontos em comum.
- Concorrentes: têm um único ponto em comum.
- Outros tipos de retas são: perpendiculares, transversal, secante e tangente.
- Além da reta, existe a semirreta e o segmento de reta.
- A semirreta tem início, mas não tem fim.
- O segmento de reta tem início e fim determinados.
- A reta orientada tem sentido positivo e sentido negativo.
- A reta numérica é um caso particular de reta orientada que organiza os números reais de forma ordenada.
- Nos estudos da geometria analítica, é possível descrever a equação geral e a equação reduzida da reta.
O que são retas?
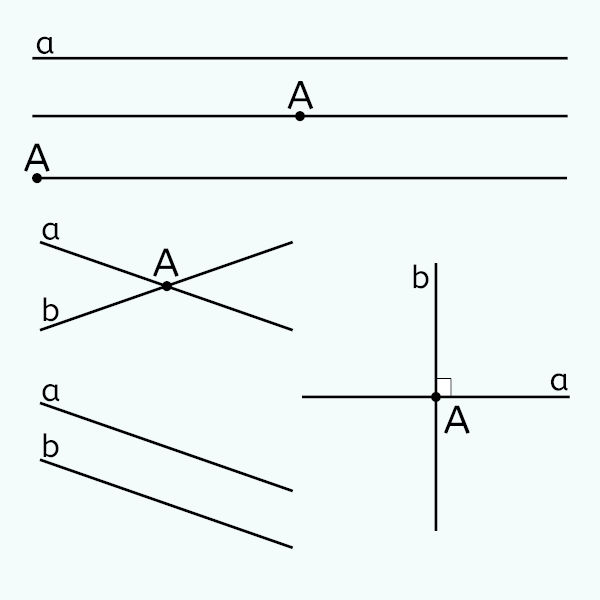
A reta é um elemento primitivo da geometria, juntamente do ponto e do plano. Ser um elemento primitivo significa que não é possível definir o conceito de reta por conceitos mais básicos, pois a reta por si só é um conhecimento que desenvolvemos de forma intuitiva.
Propriedades da reta
De forma intuitiva, podemos descrever as propriedades da reta:
- A reta é infinita e não tem extremidade.
- A reta não tem curva.
- A reta tem infinitos pontos.
- A reta é unidimensional, ou seja, tem única dimensão, que é o comprimento.
- Utilizamos letras minúsculas do alfabeto para representar a reta, como reta r, reta s, reta t.
Classificação das retas
As retas podem ser classificadas de acordo com a posição relativa entre elas. Existem três classificações possíveis: retas paralelas, retas concorrentes e retas coincidentes.
→ Retas paralelas
Duas retas são conhecidas como paralelas quando elas não têm nenhum ponto em comum, isso acontece porque elas têm mesma inclinação e geometricamente ocupam espaços diferentes.
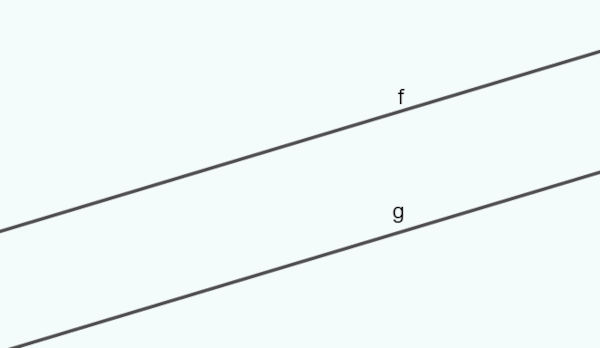
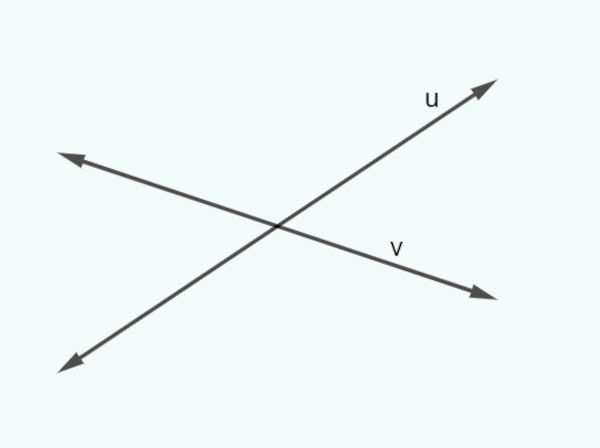
→ Retas concorrente
Duas retas são classificadas como concorrentes quando elas se encontram em um único ponto.
→ Retas coincidentes
As retas são coincidentes quando têm infinitos pontos em comum.
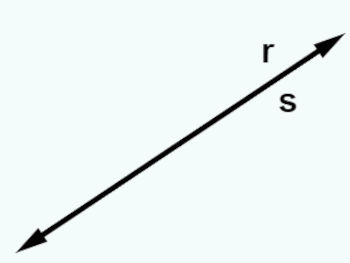
Tipos de retas
A seguir, outros casos em que as retas recebem nomes especiais.
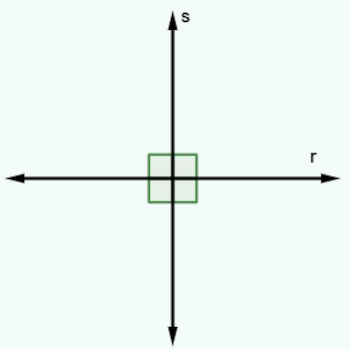
→ Retas perpendiculares
Retas perpendiculares são retas que são concorrentes e que formam um ângulo de 90º entre si.
→ Reta transversal
Reta transversal é uma reta que corta duas ou mais retas paralelas.
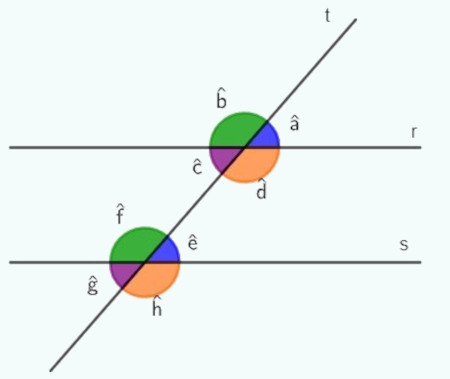
Importante: Existem propriedades importantes nos ângulos formados entre a reta transversal e as retas paralelas, pois os ângulos formatos pela reta r são congruentes aos respectivos ângulos formados pela reta s.
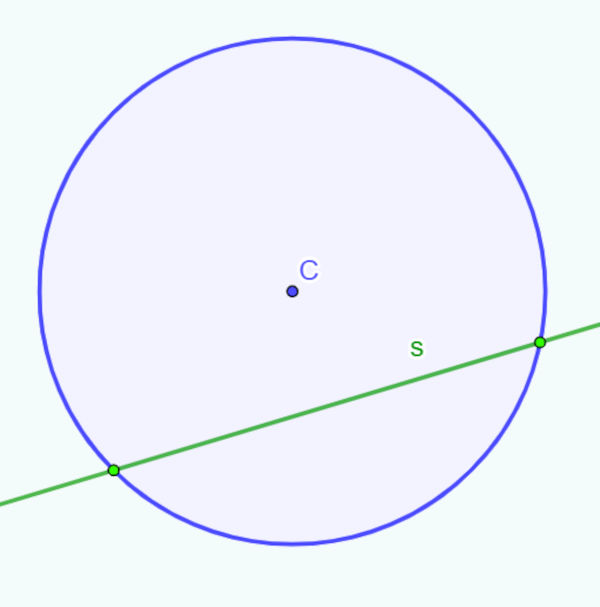
→ Reta secante
Reta secante é uma reta que intersecta determinada figura geométrica em dois ou mais pontos. Isso quer dizer que essa reta atravessa a figura geométrica.
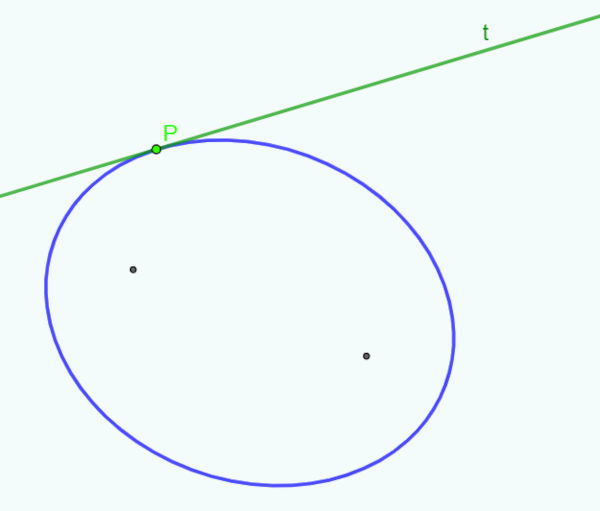
→ Reta tangente
Reta tangente é a reta que toca uma curva em um único ponto.
Reta e semirreta
Enquanto a reta não tem início nem fim determinados, a semirreta tem um início determinado, entretanto não tem um final determinado.
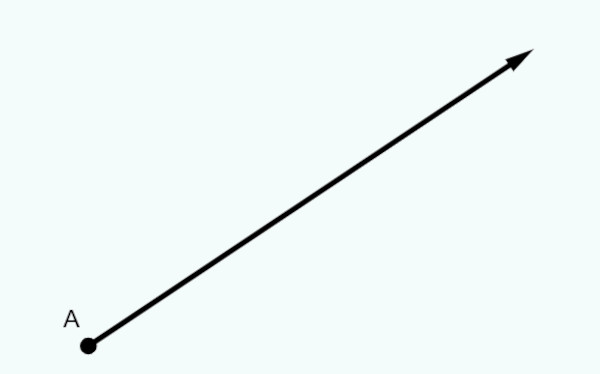
Note que a semirreta da imagem começa no ponto A, mas é infinita para o outro lado.
Reta e segmento de reta
Enquanto a reta não tem início nem fim determinados, o segmento de reta é uma parte de uma reta que é limitada dos dois lados. Sendo assim, o segmento de reta é um segmento que liga dois pontos no plano.
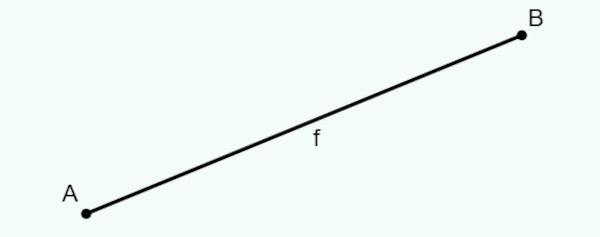
Reta numérica e reta orientada
- Reta orientada: de modo geral, a partir de determinado ponto dessa reta, temos um lado que tem sentido positivo e o outro lado que tem sentido negativo. A reta orientada é conhecida também como eixo. Por exemplo, com duas retas orientadas, podemos formar o conhecido plano cartesiano.
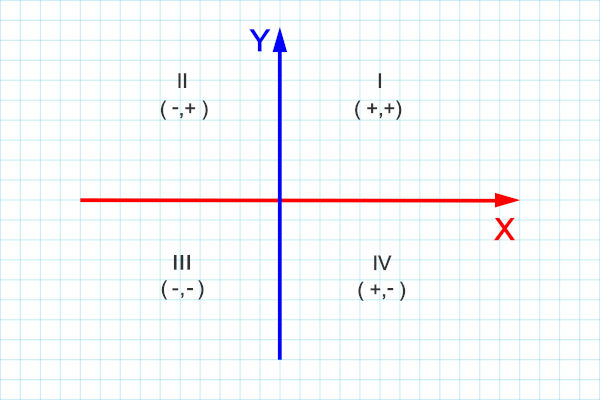
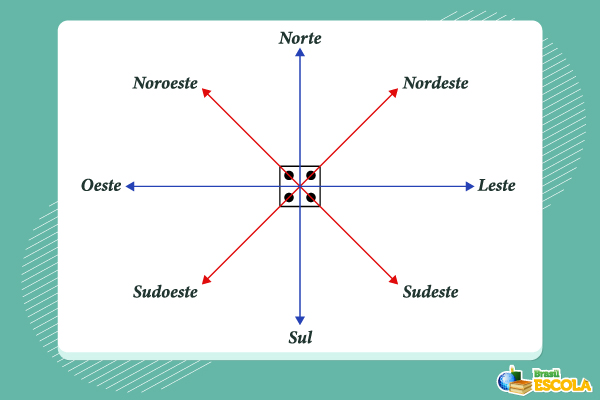
- Reta numérica: é nomeada como reta orientada por alguns autores, mas, na verdade, é um caso particular de reta orientada, pois a reta numérica nos permite representar graficamente os números reais em uma linha reta, em que cada número corresponde a um ponto específico, tornando possível visualizar melhor as operações básicas e realizar a comparação de valores. A reta numérica tem na sua origem o ponto que representa o número 0. Para a esquerda do 0, estão os números negativos de forma decrescente, e, para a direita do 0, os números positivos de forma crescente. Na reta numérica, é possível fazer a representação de todos os números reais.

Acima temos um esboço da reta numérica, mas podemos representar qualquer número nela. Por exemplo, sabemos que, entre 0 e 0,5, está o número 0,2 ou então a dízima periódica 0,252525252..., entre outros números. De forma geral, entre dois números reais existem infinitos números; logo, a reta nos permite observar e comparar os números, pois eles são representados em ordem crescente da esquerda para a direita.
Equação geral da reta
A equação geral da reta é uma maneira de descrever por uma equação o comportamento da reta quando representada no plano cartesiano. O gráfico de uma reta, quando representado no plano cartesiano, pode ser crescente ou decrescente, e a equação geral da reta é a equação:
ax + by + c = 0
Equação reduzida da reta
A equação reduzida da reta nada mais é que outra forma de representar a equação da reta e tem o mesmo objetivo da equação geral, ou seja, traçar o comportamento da reta no plano cartesiano. A equação reduzida da reta é:
y = mx + n
Acesse também: Qual é a equação paramétrica da reta?
Exercícios resolvidos sobre retas
Questão 1
Sobre a classificação das retas quanto à posição relativa no plano, marque a alternativa correta:
A) Retas concorrentes nunca têm ponto em comum.
B) Retas paralelas têm infinitos pontos em comum.
C) Retas coincidentes têm exatamente um ponto em comum.
D) Retas concorrentes têm apenas um ponto em comum.
E) Retas paralelas sempre se cruzam em um ponto.
Resolução:
Alternativa D.
Por definição, retas concorrentes têm apenas um ponto em comum.
Questão 2
Durante uma aula de Matemática, o professor Raul fez no quadro o desenho de uma linha que se estendia infinitamente para os dois lados e pediu para o aluno Heitor identificar o que era. Depois disso, ele desenhou outra figura que começava em um ponto fixo A e se estendia infinitamente apenas para um lado.
Com base nessa situação, assinale a alternativa correta:
A) A primeira figura é uma reta e a segunda é um segmento de reta.
B) A primeira figura é uma reta e a segunda é uma semirreta.
C) A primeira figura é uma semirreta e a segunda é uma reta.
D) A primeira figura é um segmento de reta e a segunda é uma reta.
E) A primeira figura é uma semirreta e a segunda é um segmento de reta.
Resolução:
Alternativa B.
A primeira figura é uma reta, já a segunda é uma semirreta.
Fontes
DANTE, Luiz Roberto. Geometria: fundamentos e aplicações. 3. ed. São Paulo: Ática, 2013.
MENES, Luiz Marcio; LELLIS, Marcelo. Matemática. São Paulo: Moderna, 2012. (8º e 9º ano)

