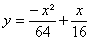As funções do 2º grau possuem diversas aplicações na Matemática e auxiliam a Física em diversas situações nos movimentos de corpos na área da Cinemática e Dinâmica. A sua lei de formação, onde f(x) = ax² + bx + c, descreve uma trajetória parabólica de concavidade voltada para cima (decrescente - ponto mínimo) ou concavidade voltada para baixo (crescente – ponto máximo). Observe a resolução de situações problemas a seguir:
Exemplo 1
O movimento de um projétil, lançado para cima verticalmente, é descrito pela equação y = – 40x² + 200x. Onde y é a altura, em metros, atingida pelo projétil x segundos após o lançamento. A altura máxima atingida e o tempo que esse projétil permanece no ar correspondem, respectivamente, a:
Resolução:
Veja o gráfico do movimento:
.jpg)
Na expressão y = –40x² + 200x os coeficientes são a = –40, b = 200 e c = 0.
Utilizaremos a expressão Yv para obter a altura máxima atingida pelo objeto:
.jpg)
O objeto atingiu a altura máxima de 250 metros.
Utilizaremos a expressão Xv para obter o tempo de subida do objeto:
.jpg)
O projétil levou 2,5s para atingir altura máxima, levando mais 2,5s para retornar ao solo, pois no movimento vertical o tempo de subida é igual ao tempo de descida. Portanto, o projétil permaneceu por 5 s no ar.
Exemplo 2
Um objeto foi lançado do topo de um edifício de 84 m de altura, com velocidade inicial de 32 m/s. Quanto tempo ele levou para chegar ao chão? Utilize a expressão matemática do 2º grau d = 5t² + 32t, que representa o movimento de queda livre do corpo.
Resolução:
O corpo percorreu a distância de 84 m que corresponde à altura do edifício. Portanto, ao substituirmos d = 84, basta resolvermos a equação do 2º grau formada, determinando o valor do tempo t, que será a raiz da equação.
.jpg)
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
