Números decimais

Os números decimais são todos os números que possuem uma parte inteira separada de uma parte decimal por uma vírgula, como 2,5 ou 0,00008. Para que façamos a leitura dos números decimais, primeiro lemos a parte inteira e depois, a parte decimal.

Leia também: Como funciona o sistema de numeração decimal?

Tópicos deste artigo

• 1 - Resumo sobre números decimais
• 2 - O que são números decimais?
• 3 - Quais são os números decimais?
• 4 - Como se lê um número decimal?
• 5 - Operações com números decimais
  • → Adição com números decimais
  • → Subtração com números decimais
  • → Multiplicação com números decimais
  • → Divisão com números decimais
• 6 - Como transformar número decimal em fração?
• 7 - Como transformar fração em número decimal?
• 8 - Exercícios resolvidos sobre números decimais

Resumo sobre números decimais

• Os números decimais são números que possuem vírgula.
• Os números decimais têm uma parte inteira e uma parte decimal.
• Primeiro, lê-se a parte inteira e depois a parte decimal.
• Podemos fazer operações de adição, subtração, multiplicação e divisão com números decimais.
• Podemos transformar um número decimal em fração removendo a vírgula do número e contando a quantidade de casas após a vírgula, para colocar o número correspondente no denominador.
• Podemos transformar uma fração em um número decimal dividindo o numerador pelo denominador.

O que são números decimais?

Números decimais são todos os números que possuem vírgula aparente, que particiona o número em uma parte inteira, e uma parte decimal diferente de zero. Eles se diferenciam dos números inteiros (não decimais) que não possuem uma parte decimal diferente de zero e cuja vírgula está “escondida” após o seu último número,sendo seguida por zeros que não alteram seu valor.

Quais são os números decimais?

Os números decimais são todos aqueles que apresentam uma parte inteira (tudo antes da vírgula) e uma parte decimal diferente de zero (tudo depois da vírgula). Alguns exemplos de números decimais são 1,25; 0,67, 1,000009 e 5.734,912.

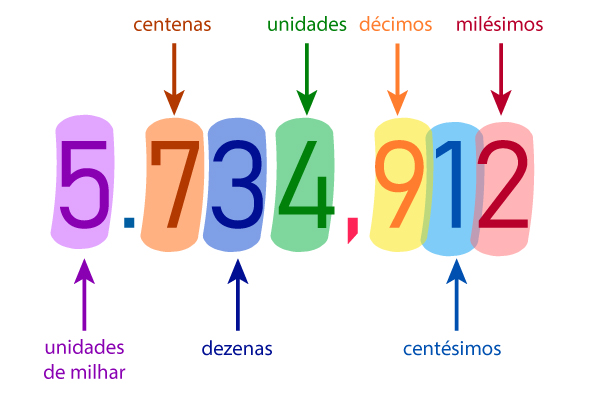
Como se lê um número decimal?

Existem diversas formas de se ler os números decimais, mas o mais recomendável é ler primeiro a parte inteira, falar vírgula (ou “e”), fazer uma pausa e depois ler a parte decimal.

Exemplos:

• 0,005 — lê-se:
  • zero vírgula zero zero cinco; ou
  • zero e zero zero cinco; ou
  • cinco milésimos.
• 1,545  — lê-se:
  • um vírgula quinhentos e quarenta e cinco; ou
  • um e quinhentos e quarenta e cinco; ou
  • um inteiro e quinhentos e quarenta e cinco milésimos.
• 12,89  — lê-se:
  • doze vírgula oitenta e nove;
  • ou doze e oitenta e nove; ou
  • doze inteiros e oitenta e nove centésimos.
• 7,6  — lê-se:
  • sete vírgula seis; ou
  • sete e seis; ou
  • sete inteiros e seis décimos.
• 1 000,43 — lê-se:
  • mil vírgula quarenta e três; ou
  • um zero zero zero vírgula quatro três; ou
  • mil e quarenta e três centésimos.

Veja também: Quais são os números racionais?

Operações com números decimais

Existem diversas operações que podem ser realizadas com números decimais, tais como adição, subtração, multiplicação e divisão.

→ Adição com números decimais

Na adição com números decimais, é necessário organizar os números de maneira que fique vírgula embaixo de vírgula, a casa das unidades fique embaixo da casa das unidades, e assim em diante com as demais casas. Depois disso, realizamos a adição normalmente.

Observação: os números que não possuem vírgula, na verdade possuem uma vírgula “escondida” no final do último número.

Exemplo:

• Some o número decimal 2,4 com o número decimal 0,2.

Primeiro, organizamos as casas decimais, depois realizamos a soma de 4 com 2 que resulta em 6, e a soma de 2 com 0 que resulta em 2. Por fim, descemos a vírgula e obtemos o resultado 2,6.

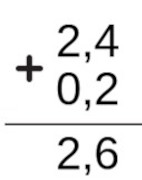
→ Subtração com números decimais

Na subtração com números decimais, é necessário organizar os números de maneira que fique vírgula embaixo de vírgula, a casa das unidades fique embaixo da casa das unidades, e assim em diante com as demais casas. Depois disso, realizamos a subtração normalmente.

Exemplo:

• Subtraia o número decimal 2,4 pelo número decimal 0,2.

Primeiro, organizamos as casas decimais, depois realizamos a subtração de 4 com 2 que resulta em 2 e a subtração de 2 com 0 que resulta em 2. Por fim, descemos a vírgula e obtemos o resultado 2,2.

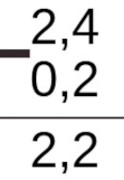
→ Multiplicação com números decimais

Na multiplicação com números decimais, é necessário organizar os números de maneira a vírgula fique embaixo da outra vírgula, a casa das unidades fique embaixo da casa das unidades, e assim em diante com as demais casas. Depois disso, realizamos a multiplicação normalmente.

Exemplo:

• Multiplique o número decimal 2,4 pelo número decimal 0,2.

Primeiro, organizamos as casas decimais, depois realizamos a multiplicação de 2 por 4 que resultou em 8 e a multiplicação de 2 por 2 que resulta em 4. Em seguida, realizamos a multiplicação de 0 por 4 que resulta em 0, e a multiplicação de 0 por 2 que resulta em 0. Por fim, somamos os números obtidos, resultando em 048. Como os dois números possuem 1 casa após a vírgula, temos então que colocar 2 casas após a vírgula no número 048, então obtemos o resultado de 0,48.

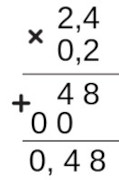
→ Divisão com números decimais

Na divisão com números decimais, quando o dividendo for maior que o divisor, multiplicaremos o dividendo e o divisor por 10, 100, 1000 até que a vírgula “fique escondida atrás do último número” e continuamos a divisão normalmente.

Exemplo:

• Divida o número decimal 2,4 pelo número decimal 0,2.

Nesse caso, o dividendo 2,4 é maior que o divisor 0,2, logo, multiplicaremos ambos por 10, resultando em 24 e 2. Assim a vírgula ficou escondida atrás do 4 e do 2. Por fim, fazemos a divisão de 24 por 2 que resulta em 12.

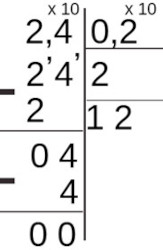
Na divisão com números decimais, quando o dividendo for menor que o divisor, multiplicaremos o dividendo por 10 (ou 100 e 1000) até que o dividendo seja maior que o divisor e adicionamos “0,”(ou “0,0” e “0,00”) no quociente, e continuamos a divisão normalmente.

Exemplo:

• Divida o número decimal 0,2 pelo número decimal 0,4.

Nesse caso, o dividendo 0,2 é menor que o divisor 0,4, então, multiplicaremos 0,2 por 10, resultando em 2, e acrescentaremos um “0,” no quociente. Por fim, fazemos a divisão de 2 por 0,4 que resulta em 5. Como já tínhamos “0,”, a divisão de 0,2 por 0,4 resulta em 0,5.

Como transformar número decimal em fração?

Podemos transformar um número decimal em fração retirando a vírgula do número e contando a quantidade de casas após a vírgula. Se tivermos uma casa após a vírgula, colocaremos no denominador o número 10, se tivermos duas casas após a vírgula, colocaremos no denominador o número 100 e assim por diante. Caso seja possível, simplificar a fração, dividindo o numerador e o denominador pelo mesmo número inteiro.

Exemplo:

• Transforme o número decimal 0,4 em fração.

Primeiro, vamos retirar a vírgula, resultando no número 4; como só tem uma casa após a vírgula, dividiremos o número 4 por 10, resultando na fração 4/10. Nesse caso podemos simplificar a fração, dividindo em cima e embaixo por 2. O resultado é 2/5.

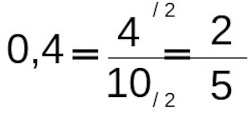
Como transformar fração em número decimal?

Podemos transformar uma fração em um número decimal fazendo a divisão do numerador pelo denominador.

Exemplo:

• Transforme a fração 2/4 em número decimal.

Para isso, dividiremos o número 2 pelo número 4, resultando em 0,5.

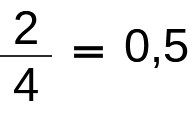
Saiba mais: Como fazer adição e subtração de frações?

Exercícios resolvidos sobre números decimais

1.  (PUC-RJ 2018) O valor de 0,5/0,05 + 0,05/0,005 é igual a:

a) 0,0005

b) 5

c) 10

d) 20

e) 25000

Resolução:

Alternativa D. Primeiro, transformaremos o primeiro termo da expressão em fração e faremos a operação de divisão entre frações:

\(\frac{0,5}{0,05}=\frac{\frac{5}{10}}{\frac{5}{100}}=\frac{5}{10}\cdot \frac{100}{5}=\frac{100}{10}=10\)

Depois, faremos o mesmo com o segundo termo:

\(\frac{0,05}{0,005}=\frac{\frac{5}{100}}{\frac{5}{1000}}=\frac{5}{100}\cdot \frac{1000}{5}=\frac{1000}{100}=10\)

Por fim, somaremos os resultados:

\(\frac{0,5}{0,05}+\frac{0,05}{0,005}=10+10=20\)

2. Encontre o resultado da expressão numérica abaixo:

\(52,3 + 0,6+1006+0,009\)

a) 1544

b) 1059,08

c) 1067,9

d) 1073,3

e) 1058,9009

Resolução:

Alternativa E.  Primeiro, organizaremos a expressão, colocando casa das unidades abaixo de casa das unidades e assim por diante com as demais casas. Vale lembrar que, no final do número 1006, temos uma vírgula e um zero escondidos.

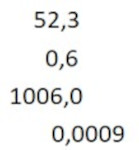
Depois, faremos a adição dos termos e podemos adicionar zeros para facilitar o somatório:

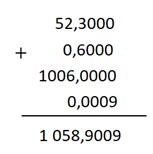
Fontes

IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos de matemática elementar – Volume 1: Conjuntos e funções 9ª edição. São Paulo: Atual Editora, 2019.

PAIVA, Manoel Rodrigues. Matemática Paiva (vol. 1). 2 ed. São Paulo: Editora Moderna Plus, 2010.