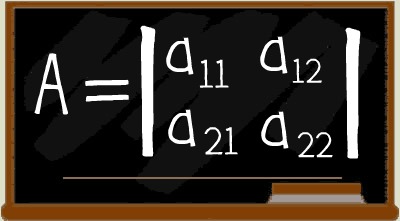Home
Matemática
Matriz e Determinante

Matriz e Determinante

A+

A-

Ouça o texto abaixo!

1x

A matriz e os determinantes não são encontrados apenas no estudo da matemática, mas também na engenharia, informática, tabelas financeiras etc. Uma matriz é um conjunto ordenado de elementos dispostos em linhas e colunas representadas respectivamente por m e n, onde n ≥ 1 e m ≥ 1.
Para representar essas linhas e colunas devemos obedecer às regras, dependendo do número de linhas e colunas a matriz recebe um nome e podemos também aplicar a elas as quatro operações.

Determinante é um tipo de matriz, mas essa deverá ter o mesmo número de linhas e o mesmo número de colunas, que é chamada de matriz quadrada. Nele não aplicamos as quatro operações, mas tem suas propriedades, como achar o valor numérico de um determinante.

Não pare agora... Tem mais depois da publicidade ;)

Por Danielle de Miranda
Graduada em Matemática
Brasil Escola

Esta é uma matriz 2x2.

Escrito por: Brasil Escola Escritor oficial Brasil Escola

Deseja fazer uma citação?

ESCOLA, Brasil. "Matriz e Determinante"; Brasil Escola. Disponível em: https://brasilescolav3.elav.tmp.br/matematica/matriz-e-determinante.htm. Acesso em 29 de outubro de 2025.

Copiar

Videoaulas

Professor ao lado do texto"Tipos de Matrizes".

📽 Reproduzindo

Professor ao lado do texto"Multiplicação de Matrizes".

📽 Reproduzindo

Professor ao lado do texto"Condição para Multiplicação de Matrizes".

📽 Reproduzindo

"Determinante de matriz de ordem 1, 2 e 3" escrito sobre fundo verde ao lado da imagem do professor

📽 Reproduzindo

Artigos de Matriz e Determinante

Adição e Subtração de Matrizes

Aplicação das matrizes nos vestibulares

É importante saber como proceder no vestibular quando você se deparar com questões que envolvem matrizes, pois a aplicação das matrizes permeia diversos conceitos em apenas um enunciado.

Calculando o cofator

Diante da dificuldade de se calcular o determinante de matrizes com ordens superiores a 3, surge o cofator, uma expressão utilizada no teorema de Laplace que auxilia nos cálculos de determinantes.

Classificação de um sistema linear

Classificando as soluções de um sistema linear escalonado

A classificação de sistemas lineares escalonados ocorre por meio da análise de suas equações e suas incógnitas. Estas informações nos auxiliam a identificar que tipo de conjunto solução obteremos.

Determinante de matriz: Regra de Chió

Sabemos que a maioria das regras que temos para o cálculo de determinantes de matrizes é aplicada apenas a matrizes de ordem igual ou menor que 3. É possível calcular os determinantes de matrizes de ordem maior, porém esse cálculo oferece grande dificulda

Determinante de uma matriz quadrada é um número real que pode obter vários significados dependendo do contexto. Seu cálculo passa por processos específicos.

Discussão e análise do sistema linear

A discussão dos sistemas lineares consiste em analisar parâmetros dos coeficientes em relação ao determinante da matriz que representa os coeficientes das equações; e, através desses parâmetros, classificar os sistemas quanto às suas soluções.

Equação linear

Equações com matrizes – Equações envolvendo matrizes

Existência de uma matriz inversa

Matriz é uma estrutura matemática disposta em tabela e que possui as operações de adição, subtração e multiplicação muito bem definidas.

Matriz identidade

A matriz identidade é a matriz quadrada em que os elementos da diagonal principal são iguais a 1 e os demais elementos são iguais a 0.

A matriz inversa da matriz M é a matriz M-1, em que a multiplicação entre M e M-1 é igual à matriz identidade In. Para encontrar a inversa, basta utilizar técnicas de equação.

Matriz simétrica

Matriz simétrica é a que possui cada elemento na posição ij igual ao elemento na posição ji para todo i e todo j.

Matriz transposta

Matriz transposta dá-se quando mudamos a posição das linhas e das colunas de uma matriz. A notação utilizada para matriz transposta de A é At.

Matriz triangular

A matriz triangular é uma matriz quadrada em que todos os elementos que estão acima ou abaixo da diagonal principal são iguais a zero.

Menor Complementar

Multiplicação de matrizes

Para calcular a multiplicação entre duas matrizes, utilizamos um algoritmo. A multiplicação A·B é possível quando o número de colunas de A é igual ao número de linhas de B.

Multiplicando um número Real por uma Matriz

Processo para resolução de um sistema linear m x n

Propriedades dos Determinantes

Regra de Cramer

Regra de Cramer é um método desenvolvido para encontrar as soluções de sistemas lineares com a utilização do cálculo do determinante de matrizes.

Regra de Sarrus

A Regra de Sarrus é um método muito utilizado para o cálculo de determinante de matrizes quadradas de ordem 3.

Relação entre Matriz e Sistemas Lineares

Sistema linear homogêneo

Sistemas lineares

Sistemas lineares são formados por duas ou mais equações lineares que possuem suas incógnitas relacionadas. Eles podem ser resolvidos por meio de diferentes métodos.

Solução de Sistemas Lineares

Sistemas lineares consistem em um conjunto de equações que possuem correlação entre as incógnitas. Sendo assim, o conjunto solução de um sistema linear é composto pelo valor das incógnitas que satisfazem todas as equações desse sistema.

Teorema de Binet

Teorema de Binet é utilizado para calcular o determinante de uma matriz produto. Dada duas matrizes, A e B, quadradas de mesma ordem, então, det(A) · det(B) = det(A · B).

Teorema de Laplace

Nos cálculos dos determinantes, as regras práticas se estendem, em sua maioria, apenas para as matrizes quadradas de ordem igual ou menor que três. Para calcular o determinante das demais, é necessário usar o teorema de Laplace.

Tipos de Matrizes