Tunelamento quântico

O tunelamento quântico é um fenômeno no qual uma partícula tem uma probabilidade não nula de atravessar uma barreira de potencial maior que a sua própria energia. Esse fenômeno é capaz de explicar como ocorre a desintegração radioativa, mais especificamente o decaimento alfa, além de permitir a construção do microscópio de tunelamento, instrumento muito mais eficaz que o microscópio óptico comum.

Leia também: Afinal, o que a física quântica estuda?

Resumo sobre o tunelamento quântico

• O tunelamento quântico é um fenômeno no qual uma partícula tem uma probabilidade não nula de atravessar uma barreira de potencial maior que a sua própria energia.
• O tunelamento quântico só pode ser previsto à luz da mecânica quântica, uma teoria probabilística que permite tratar a partícula como onda.
• O microscópio de tunelamento é um dispositivo que permite obter imagens de alta resolução de superfícies.
• São aplicações do tunelamento quântico o diodo túnel, a junção de Josephson e o curral quântico.
• A probabilidade de ocorrência do tunelamento quântico é dada pelo coeficiente de transmissão: \(T \approx e^{-2 \cdot b \cdot L}\), em que \(b = \sqrt{\dfrac{8 \cdot \pi^2 \cdot m \cdot (U_b - E)}{h^2}}\).
• Físicos importantes na descoberta do tunelamento quântico: Friedrich Hund, George Gamow e Max Born.

O que é tunelamento quântico?

O tunelamento quântico, ou efeito túnel, é um fenômeno da mecânica quântica (ou física quântica) no qual uma partícula de dimensões atômicas ou subatômicas tem uma probabilidade finita de atravessar uma barreira de potencial, mesmo que sua energia cinética seja menor que a energia potencial da barreira. Esse tipo de fenômeno não pode ser explicado pela mecânica clássica (ou mecânica newtoniana), tendo em vista que a mecânica quântica é uma teoria probabilística e sua formulação permite tratar as partículas microscópicas a partir de uma abordagem ondulatória (ondas de matéria).

Como ocorre o tunelamento quântico?

Primeiramente precisamos entender a noção de barreira de potencial na mecânica clássica. Suponha que uma bola deslize sem atrito em um plano horizontal em direção a uma colina. Quando a bola começa a subir a colina, parte da energia cinética K é transformada em energia potencial gravitacional U. Quando a bola chega ao alto da colina, a energia é U_b. Isso significa que a bola só conseguirá chegar ao outro lado da colina se a energia mecânica inicial E  for maior que U_b. Se E < U_b, a bola para de subir antes de chegar ao alto da colina e escorrega de volta para a esquerda.

Dizemos que a colina se comporta como uma barreira de energia potencial, ou somente uma barreira de potencial.

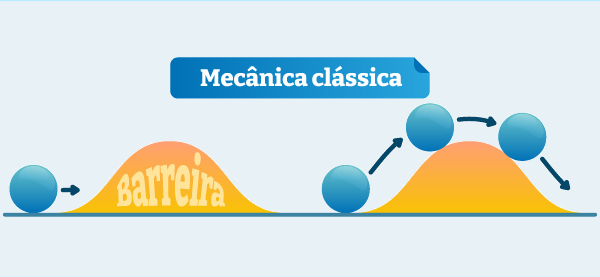
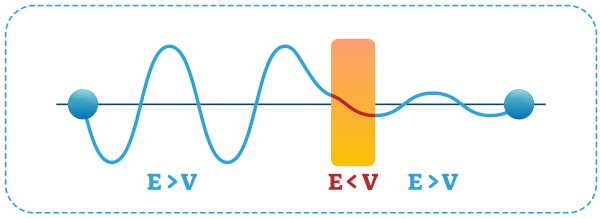
Por outro lado, nos sistemas quânticos as coisas são um pouco diferentes. Consideremos agora uma barreira de potencial qualquer V para um elétron que está em movimento com energia inicial E e tente atravessá-lo. Se E < V, esperamos que o elétron não consiga passar pela barreira e que o sentido do movimento do elétron se inverta, como no caso da bola. Porém, outra coisa surpreendente acontece. Como o elétron é uma onda de matéria, existe uma probabilidade finita de que atravesse a barreira e apareça do outro lado, movendo-se para a direita com energia E como se nada tivesse acontecido. É o chamado tunelamento quântico.

No seguinte gráfico, a curva periódica à esquerda da barreira é uma combinação da onda de matéria incidente e da onda refletida. No interior da barreira, a densidade de probabilidade de encontrar o elétron diminui exponencialmente. À direita da barreira, a densidade de probabilidade tem um valor pequeno, mas não nulo, e permanece constante. Isso significa que a onda é parcialmente transmitida através da barreira e um elétron pode ser detectado em qualquer ponto à direita da barreira, embora com baixa probabilidade.

Microscópio de tunelamento

O microscópio de tunelamento é um dispositivo criado por Gerd Binnig e Heinrich Rohrer que permite obter imagens de alta resolução de superfícies as quais os microscópios ópticos não são capazes de observar, devido ao limite do comprimento de onda da luz utilizada.

Ele opera da seguinte forma: uma ponta metálica, montada em barras de quartzo, é colocada nas proximidades da superfície a ser examinada. Uma pequena diferença de potencial, da ordem de 10 mV, é aplicada entre a ponta e a superfície. O quartzo é um material piezoelétrico: quando uma DDP (diferença de potencial) é aplicada às extremidades de uma barra do material, as dimensões da barra variam ligeiramente. Essa propriedade é usada para mudar o comprimento das barras de modo a fazer a ponta varrer a superfície da amostra a ser examinada e se aproximar e se afastar da superfície.

Quando a ponta está próxima da superfície, elétrons da amostra podem atravessar a barreira, graças ao tunelamento quântico, dando origem a uma corrente elétrica, a chamada corrente de tunelamento.

Enquanto a ponta varre a superfície da amostra, um sistema de realimentação é usado para ajustar a posição vertical da ponta de modo a manter constante a corrente de tunelamento. Isso significa que a distância entre a ponta e a superfície também permanece constante durante a varredura. O sinal de saída do aparelho é um registro da altura da ponta em relação a um nível de referência e, portanto, um registro do relevo da superfície da amostra.

Leia também: Transformação de Lorentz — equações que relacionam as coordenadas no espaço-tempo de um evento relativístico

Aplicações do tunelamento quântico

Além do microscópio de tunelamento, o efeito túnel tem muitas aplicações tecnológicas, a saber:

• Diodo túnel ou diodo Esaki: dispositivo no qual se faz variar uma corrente de elétrons controlando a altura de uma barreira. Como isso pode ser feito rapidamente (a intervalo de menos de 5 ps), ele é útil em aplicações que exigem uma resposta rápida do circuito.

• Junção de Josephson: dispositivo eletrônico baseado no efeito túnel em supercondutores (materiais que, a temperaturas extremamente baixas, conduzem corrente elétrica sem resistência).

• Curral quântico: procedimento extremamente sensível que utiliza um microscópio de tunelamento para manipular átomos e moléculas.

Qual é a probabilidade de ocorrência do tunelamento quântico?

Sendo m  a massa da partícula, h a constante de Planck, L  a largura da barreira e U_b - E a diferença entre a energia máxima da barreira e a energia da partícula, a probabilidade de ocorrência do tunelamento quântico é dada pelo coeficiente de transmissão T, determinada por:

\(T \approx e^{-2 \cdot b \cdot L}\),

Em que:

\(b = \sqrt{\dfrac{8 \cdot \pi^2 \cdot m \cdot (U_b - E)}{h^2}} \)

Assim, por exemplo, se T=0,02, isso significa que, para cada 1000 elétrons que colidem com a barreira, 20 atravessam e 980 são refletidos.

História do tunelamento quântico

A descoberta do tunelamento quântico foi o grande responsável por dar uma compreensão mais profunda de como ocorria a desintegração radioativa, fenômeno pelo qual alguns elementos químicos pesados são capazes de emitir partículas que estavam fortemente ligadas aos seus núcleos atômicos. Com a descrição da mecânica clássica, seria impossível que esses elementos emitissem essas partículas.

Em 1927, o físico alemão Friedrich Hund foi o primeiro a obter soluções da equação de Schrödinger, que indicavam a existência do tunelamento quântico em seus trabalhos sobre o potencial de poço duplo. No ano seguinte, o físico estadunidense George Gamow resolveu a teoria do decaimento alfa de um núcleo via tunelamento. Influenciado pelo trabalho de Gamow, o físico alemão Max Born desenvolveu a teoria do tunelamento quântico, percebendo-a como uma consequência da natureza quântica, aplicável não só à física nuclear, mas também a vários outros sistemas quânticos.

Fontes

CARRON, Wilson; GUIMARÃES, Osvaldo. As faces da física (vol. único). 1. ed. Moderna, 1997.

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Óptica e Física Moderna (vol. 4). 9 ed. Rio de Janeiro, RJ: LTC, 2012.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Óptica, Relatividade e Física Quântica (vol. 4). 2 ed. São Paulo: Editora Blucher, 2014.