Colisão (Física)

  Colisão é o choque entre corpos no qual ocorre a conservação da quantidade de movimento. Uma das aplicações mais importantes do conceito de quantidade de movimento é encontrada no estudo de interações de curta duração, entre partes de um sistema (ou conjunto) de corpos, como ocorre em uma explosão ou em uma colisão. Em toda colisão há a conservação da quantidade de movimento do sistema.

  O que diferencia os tipos de colisões é a conservação da energia cinética. Se a energia cinética se conserva, a colisão será elástica. Se a energia cinética não se conserva, a colisão será inelástica. E se a energia cinética é totalmente perdida, a colisão será perfeitamente inelástica.

Leia também: Afinal, o que é quantidade de movimento?

Resumo sobre colisão

• Colisão é o fenômeno que ocorre num intervalo de tempo curto em que corpos se chocam e ocorre a conservação da quantidade de movimento. 
• Ela pode ser elástica, inelástica ou perfeitamente inelástica.
• • Colisão elástica: ocorre quando há a conservação da energia cinética.
  • Colisão inelástica: ocorre quando não há a conservação da energia cinética.
  • Colisão perfeitamente inelástica: ocorre quando há a perda total da energia cinética.

• Para toda colisão: \(\sum Q_{\text{antes}} = \sum Q_{\text{depois}} \)
• Colisão elástica: \(\sum E_{c\,(\text{antes})} = \sum E_{c\,(\text{depois})}\)
• Colisão inelástica: \(\sum E_{c\,(\text{antes})} > \sum E_{c\,(\text{depois})} \)
• Coeficiente de restituição: \(e = \frac{\text{Velocidade relativa de afastamento}}{\text{Velocidade relativa de aproximação}} \)

O que é colisão?

Uma colisão (ou choque) é um evento que ocorre num intervalo de tempo muito pequeno, num sistema isolado de forças externas que apresenta a conservação da quantidade de movimento do sistema composto pelos corpos que colidem.

Tipos de colisão

As colisões podem ser elásticas, inelásticas ou perfeitamente inelásticas.

→ Colisão elástica

A colisão elástica ocorre quando há a conservação da energia cinética, ou seja, a energia cinética do sistema antes da colisão é igual à energia cinética após a colisão. Quando dois corpos que se movem em sentidos contrários sofrem uma colisão elástica, os corpos vão para direções contrárias depois da colisão, sem haver a deformação deles e sem ocorrer a perda da energia cinética do sistema. Um exemplo de colisão praticamente elástica é a colisão entre as bolas de bilhar, feitas de um material duro que praticamente não se deforma durante a colisão.

→ Colisão inelástica

Colisão inelástica ocorre quando não há a conservação da energia cinética do sistema, ou seja, a energia cinética do sistema antes da colisão não é igual à energia cinética após a colisão. A maioria das colisões é inelástica. Nesse tipo de colisão, a energia pode ser transformada em outro tipo de energia, por exemplo, em energia térmica, resultando no aumento da temperatura dos objetos que sofreram a colisão, ou em energia sonora, resultando em um som alto decorrente da colisão.

→ Colisão perfeitamente inelástica

Às vezes, os corpos que sofrem a colisão permanecem unidos após ela. Nesses casos, a colisão é denominada perfeitamente inelástica e apresenta perda máxima da energia cinética.

Acesse também: Qual é a lei de conservação de quantidade de movimento?

Fórmulas da colisão

Para todos os tipos de colisões, temos que o somatório da quantidade de movimento do sistema antes da colisão é igual ao somatório da quantidade de movimento do sistema depois da colisão:

\(\sum Q_{\text{antes}} = \sum Q_{\text{depois}} \)

Já quanto à energia cinética, temos que:

• Colisão elástica: o somatório da energia cinética do sistema antes da colisão é igual ao somatório da energia cinética do sistema depois da colisão:

\(\sum E_{c\ (\text{antes})} = \sum E_{c\ (\text{depois})} \)

• Colisão inelástica: o somatório da energia cinética do sistema antes da colisão é maior que o somatório da energia cinética do sistema depois da colisão:

\(\sum E_{c\ (\text{antes})} > \sum E_{c\ (\text{depois})} \)

Processo de colisão na Física

As colisões podem ocorrer com um corpo em movimento e outro parado, podem ocorrer com corpos se movendo em sentidos contrários ou com corpos se movendo no mesmo sentido. Podemos separar esse evento em três grandes momentos: o instante antes da colisão, o instante durante a colisão e o instante depois da colisão. Em todos os instantes, a quantidade de movimento é conservada.

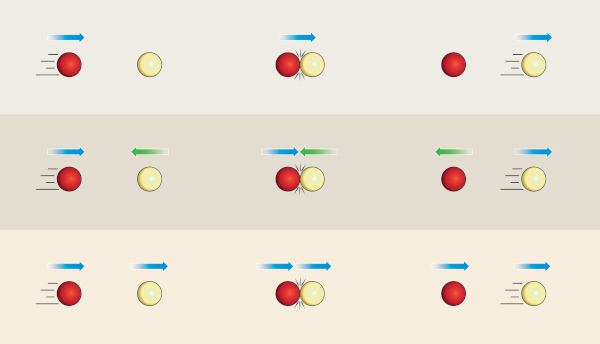
Coeficiente de restituição

Uma maneira prática de identificar se uma colisão é elástica, inelástica ou perfeitamente inelástica consiste em tomar por base a velocidade relativa de afastamento (depois) e a velocidade relativa de aproximação (antes). A relação entre os módulos dessas duas velocidades chama-se coeficiente de restituição (e):

\(e = \frac{\text{Velocidade relativa de afastamento}}{\text{Velocidade relativa de aproximação}} \)

Assim, de acordo com o valor do coeficiente de restituição, obtemos o tipo de colisão:

• Colisão elástica: e = 1
• Colisão inelástica: e < 1
• Colisão perfeitamente inelástica: e = 0

A seguir, separamos uma tabela que resume as diferenças básicas entre colisões elásticas, inelásticas e perfeitamente inelásticas:

	Colisão elástica	Colisão inelástica	Colisão perfeitamente inelástica
Coeficiente de restituição	e = 1	0 < e < 1	e = 0
Energia	Conserva-se	Dissipação parcial	Dissipação máxima
Quantidade de movimento	Constante	Constante	Constante

Exercícios resolvidos sobre colisão

Questão 1

(Fuvest) Um vagão, A, de 10.000 kg de massa, move-se com velocidade igual a 0,4 m/s sobre trilhos horizontais, sem atrito, até colidir com outro vagão, com massa de 20.000 kg, inicialmente em repouso. Após a colisão, o vagão A fica parado. A energia cinética final do vagão B vale:

A) 100 J

B) 200 J

C) 400 J

D) 800 J

E) 1600 J

Resolução:

Alternativa C.

Usando a conservação da quantidade de movimento:

\(\sum Q_{\text{antes}} = \sum Q_{\text{depois}}\)

\(m_A \cdot v_A = m_B \cdot v_B \)

\(0{,}4 \cdot 10.000 = 20.000 \cdot v_B \)

\(v_B = \frac{4000}{20.000} \)

\(v_B=0,2 m/s\)

Então, a energia cinética final do vagão B será:

\(E_{c(B)} = \frac{m_B \cdot v_B^2}{2} \)

\(E_{c(B)} = \frac{20.000 \cdot (0,2)^2}{2} \)

\(E_{c(B)} = 400\ \text{J} \)

Questão 2

(E. F. E. Itajubá-MG) Uma esfera de 2,0 kg de massa é solta, a partir do repouso, de uma altura de 9,0 m e, após bater no solo, retorna a uma altura de 4,0 m. Considerando g = 10 m/s², determine:

A) o tipo de choque;

B) o coeficiente de restituição nesse choque;

C) a perda de energia cinética no choque.

Resolução:

A) É uma colisão inelástica, pois não houve conservação da energia cinética.

B) Aplicando o teorema da conservação da energia mecânica no intervalo anterior à colisão, obtemos:

\(m \cdot g \cdot h_i = \frac{m \cdot v_{\text{antes}}^2}{2}\)

\(v_{\text{antes}} = \sqrt{2 \cdot g \cdot h_i} \)

Da mesma forma, concluímos que:

\(v_{\text{depois}} = \sqrt{2 \cdot g \cdot h_f} \)

As velocidades da esfera, antes e depois da colisão, são as próprias velocidades relativas, uma vez que o solo permanece em repouso. Portanto:

\(e = \frac{v_{\text{depois}}}{v_{\text{antes}}} \)

\(e = \frac{\sqrt{2 \cdot g \cdot h_f}}{\sqrt{2 \cdot g \cdot h_i}} \)

\(e = \sqrt{\frac{h_f}{h_i}} \)

\(e = \sqrt{\frac{4}{9}} \)

\(e = \frac{2}{3}\)

\(e=0,667\)

C) A energia mecânica antes da colisão é dada por:

\(E_{m\ (\text{antes})} = m \cdot g \cdot h_i \)

\(E_{m\ (\text{antes})} = 2 \cdot 10 \cdot 9 \)

\(E_{m\ (\text{antes})} = 180\ \text{J}\)

E a energia mecânica depois da colisão é dada por:

\(E_{m\ (\text{depois})} = m \cdot g \cdot h_f \)

\(E_{m\ (\text{depois})} = 2 \cdot 10 \cdot 4 \)

\(E_{m\ (\text{depois})} = 80\ \text{J} \)

Portanto, a perda de energia será:

\(E_{m\ (\text{antes})} - E_{m\ (\text{depois})} = 180 - 80 \)

\(E_{m\ (\text{antes})} - E_{m\ (\text{depois})} = 100\ \text{J}\)

Créditos de imagem

^[1] Sharayanan / Wikimedia Commons (reprodução)

^[2] No-w-ay / H. Caps / Wikimedia Commons (reprodução)

Fontes

CARRON, Wilson; GUIMARÃES, Osvaldo. As faces da física (vol. único). 1. ed. Moderna, 1997.

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica (vol. 1). 9 ed. Rio de Janeiro, RJ: LTC, 2012.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.