Resistência do ar

A resistência do ar é uma força provocada pela colisão entre um corpo em movimento e as moléculas do ar, retardando do movimento desse corpo. Ela é proporcional ao coeficiente de arrasto, à massa específica do fluido, à área da seção reta efetiva do corpo e à velocidade do corpo.

Leia também: Queda livre — queda dos corpos sem o efeito da força de atrito com o ar

Resumo sobre resistência do ar

• A resistência do ar é uma força que dificulta o movimento dos corpos no ar.
• A causa da resistência do ar são as colisões das moléculas do ar com o corpo em movimento.
• A resistência do ar funciona com base na terceira lei de Newton.
• Os automóveis e aeronaves são influenciados pela resistência do ar.
• O módulo da resistência do ar é calculado pela metade do produto entre o coeficiente de arrasto, a massa específica do fluido, a área da seção reta efetiva do corpo e o quadrado da velocidade do corpo.

O que é a resistência do ar?

Também conhecida como força de resistência do ar, a resistência do ar é uma força de resistência que o ar faz num corpo que está se movimentando, ou seja, uma força que se contrapõe ao movimento dos corpos.

Quanto maior for a área da superfície externa do corpo ou o coeficiente de arrasto, ou mais denso for o corpo, ou maior for a velocidade do corpo, desde que as demais grandezas permaneçam constantes, maior será a resistência do ar.

O que causa a resistência do ar?

A resistência do ar é causada pela colisão das moléculas do ar com o corpo em movimento. Quando isso acontece, surge uma força que se opõe a esse movimento.

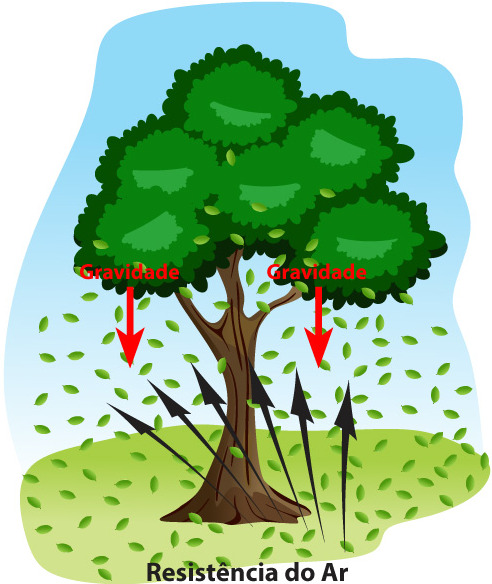
Quanto maior for a área da superfície externa do corpo, maior será a quantidade de colisões e maior será a resistência do ar e mais tempo o corpo levará para atingir o solo em uma queda. Por isso, uma folha de papel aberta demora mais tempo para atingir o solo que uma bolinha de papel amassada.

Veja também: Você sabe o que é força de arraste?

Como funciona a resistência do ar?

A resistência do ar funciona com base na terceira lei de Newton (princípio da ação e reação), que afirma que, ao aplicarmos uma força de ação sobre um corpo, ocorrerá uma força de reação em sentido oposto.

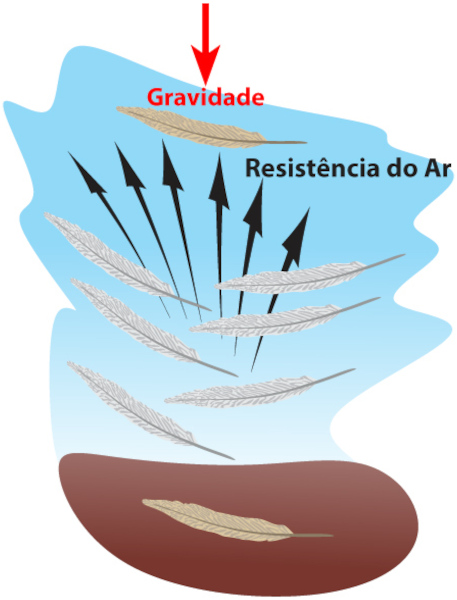
Isso significa que um corpo, quando se movimenta, colide com as moléculas de ar, realizando uma força de ação sobre elas. Em resposta, essas moléculas fazem uma força de reação em sentido contrário, retardando o movimento do corpo.

Exemplos de resistência do ar

Existem diversos exemplos de resistência do ar em nosso cotidiano. Pensando nisso, selecionamos alguns abaixo:

• A resistência do ar influencia na aerodinâmica dos automóveis e aeronaves.
• As balas, quando atiradas, têm sua velocidade retardada pela resistência do ar.
• Os capacetes de ciclistas e carros esportivos têm um design que diminui a influência da resistência do ar em suas velocidades.
• No paraquedismo, a resistência do ar diminui a velocidade do esportista, retardando a sua queda.
• Em um experimento, Arquimedes provou que, sem a resistência do ar, uma folha e uma pedra caindo demorariam o mesmo tempo para atingir o solo.

Acesse também: Como funcionam os carros de corrida?

Fórmula da resistência do ar

\(D = \frac{1}{2} \cdot C \cdot \rho \cdot A \cdot v^2 \)

• D → módulo da força de arrasto ou força de resistência do ar, medido em em Newton [N].
• C → coeficiente de arrasto, depende da forma do corpo e geralmente varia entre 0,4 e 1.
• ρ → massa específica do fluido, medida em quilograma por metro cúbico [kg/m³].
• A  → área da seção reta efetiva do corpo (área de uma seção reta perpendicular à velocidade), medida em metros quadrados [m²].
• v → velocidade do corpo, medida em metros por segundo [m/s].

Exercícios resolvidos sobre resistência do ar

Questão 1

(UFRS) Selecione a alternativa que preenche corretamente as lacunas do texto abaixo, na ordem em que elas aparecem.

Na sua queda em direção ao solo, uma gota de chuva sofre o efeito da resistência do ar. Essa força de atrito é contrária ao movimento e aumenta com a velocidade da gota. No trecho inicial da queda, quando a velocidade da gota é pequena e a resistência do ar também, a gota está animada de um movimento _____. Em um instante posterior, a resultante das forças exercidas sobre a gota torna-se nula. Esse equilíbrio de forças ocorre quando a velocidade da gota atinge o valor que torna a força de resistência do ar igual, em módulo, _____ da gota. A partir desse instante, a gota _____.

A) acelerado – ao peso – cai com velocidade constante    

B) uniforme – à aceleração – cai com velocidade decrescente

C) acelerado – ao peso – pára de cair     

D) uniforme – à aceleração – pára de cair

Resolução:

Alternativa A.

Na sua queda em direção ao solo, uma gota de chuva sofre o efeito da resistência do ar. Essa força de atrito é contrária ao movimento e aumenta com a velocidade da gota. No trecho inicial da queda, quando a velocidade da gota é pequena e a resistência do ar também, a gota está animada de um movimento acelerado. Em um instante posterior, a resultante das forças exercidas sobre a gota torna-se nula. Esse equilíbrio de forças ocorre quando a velocidade da gota atinge o valor que torna a força de resistência do ar igual, em módulo, ao peso da gota. A partir desse instante, a gota cai com velocidade constante.

Questão 2

(UFSM) Devido à resistência do ar, as gotas de chuva caem com velocidade constante a partir de certa altura. O módulo da força resistiva do ar é dado por F = A ∙ v², onde A é uma constante de valor 8 ∙ 10^-6 Ns²/m² e v é o módulo da velocidade. Nessas circunstâncias, uma gota cujo módulo do peso vale 3,2 ∙ 10^-7N  atinge o solo com velocidade de módulo, em m/s, de:

A) 4 ∙ 10^-2

B) 2 ∙ 10^-1

C) 4 ∙ 10^-1

D) 2

E) 4

Resolução:

Alternativa B.

Calcularemos a velocidade que a gota de chuva atinge o solo usando a fórmula da força de resistência do ar fornecida pelo enunciado:

\(F= A \cdot v^2\)

\(3{,}2 \cdot 10^{-7} = 8 \cdot 10^{-6} \cdot v^2 \)

\(v^2 = \dfrac{3{,}2 \cdot 10^{-7}}{8 \cdot 10^{-6}} \)

\(v^2 = 0{,}4 \cdot 10^{-7 + 6}\)

\(v^2=0,4 \cdot 10^{-1}\)

\(v^2 = 4 \cdot 10^{-1} \cdot 10^{-1}\)

\(v^2 = 4 \cdot \left(10^{-1}\right)^2\)

\(v = \sqrt{4 \cdot \left(10^{-1}\right)^2} \)

\(v=2 \cdot 10^{-1} m/s\)

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Gravitação, Ondas e Termodinâmica (vol. 2). 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Fluidos, Oscilações e Ondas, Calor (vol. 2). 5 ed. São Paulo: Editora Blucher, 2015.