Lei de Snell

A lei de Snell é uma das leis fundamentais da Óptica que descreve matematicamente o fenômeno da refração da luz. Nesse fenômeno, quando os raios luminosos atravessam meios com diferentes índices de refração, temos a sua mudança de velocidade de propagação.

Leia também: Afinal, o que é a refração da luz?

Tópicos deste artigo

• 1 - Resumo sobre a lei de Snell
• 2 - O que é a lei de Snell?
• 3 - O que diz a lei de Snell?
• 4 - Fórmula da lei de Snell
• 5 - Quem criou a lei de Snell?
• 6 - Exercícios resolvidos sobre a lei de Snell

Resumo sobre a lei de Snell

• A lei de Snell é uma das leis fundamentais da Óptica.
• Ela explica o fenômeno da refração dos feixes de luz.
• Caso a luz atravesse de um meio mais denso para um meio menos denso, temos aumento na velocidade de propagação da luz no meio, e o ângulo de refração afasta-se da normal.
• Caso a luz atravesse de um meio menos denso para um mais denso, temos diminuição da velocidade de propagação da luz no meio, e o ângulo de refração aproxima-se da normal.
• A fórmula da lei de Snell é dada pelo produto do índice de refração do meio pelo seno do ângulo de incidência (ou refração).
• A lei de Snell foi desenvolvida por Willebrord Snell van Royen.

O que é a lei de Snell?

Também chamada de lei da refração, a lei de Snell é a lei que descreve o comportamento da luz quando ela se propaga entre meios de diferentes índices de refração.

Quando a luz é incidida sobre uma superfície, com índice de refração diferente do meio em que ela já se encontrava, ela sofre o fenômeno da refração, alterando a sua velocidade de propagação e o seu ângulo de propagação (chamado de ângulo de refração), conforme demonstrado na imagem:

O que diz a lei de Snell?

A lei de Snell pode ser enunciada da seguinte forma:

O raio refratado está no plano de incidência e tem um ângulo de refração que está relacionado ao ângulo de incidência  através da equação da lei de Snel, em que  e  são constantes adimensionais, denominadas índices de refração, que dependem do meio onde a luz está se propagando.

Fundamentos da Física: Óptica e Física Moderna (vol. 4)

Isso significa que o raio refratado está sempre no plano de incidência, formando um ângulo de refração (ângulo em que a luz sai do meio) correlacionado com o ângulo de incidência (ângulo em que a luz entra no meio). Além disso, também significa que os índices de refração têm seus valores variados de acordo com o tipo de meio em que a luz está se propagando. Por exemplo, alguns índices de refração de meios são os seguintes:

• Índice de refração do ar: = 1,00
• Índice de refração da água: \(\approx\) 1,33
• Índice de refração do vidro: \(\approx\) 1,52
• Índice de refração do diamante: \(\approx\) 2,40

Consequentemente, esses índices de refração do meio influenciam na velocidade de propagação da luz no meio e no ângulo de refração, de modo que:

• Quando a luz passa de um meio de maior indice de refração (mais denso) para um meio de menor índice de refração (menos denso), a velocidade de propagação da luz no meio aumenta, e o ângulo de refração afasta-se da normal.

• Quando a luz passa de um meio de menor índice de refração (menos denso) para um meio de maior indice de refração (mais denso), a velocidade de propagação da luz no meio diminui, e o ângulo de refração aproxima-se da normal.

Confira também: Qual é a lei de Brewster?

Fórmula da lei de Snell

\(n_1 \cdot \sin \theta_1 = n_2 \cdot \sin \theta_2\)

•  n₁ → índice de refração do meio 1.
• sin θ₁ → seno do ângulo de incidência, medido em graus.
•  n₂ → índice de refração do meio 2.
•  sin θ₂ → seno do ângulo de refração, medido em graus.

Quem criou a lei de Snell?

Atualmente também conhecida como lei de Snell-Descartes, a lei de Snell foi criada em meados de 1621 pelo astrônomo e matemático Willebrord Snell van Royen (1580-1626), também chamado de Willebrord Snellius, contudo, seus manuscritos nunca foram publicados e estão atualmente perdidos.

Apenas em 1637, muitos anos após sua morte, a lei foi publicada pelo filósofo, físico e matemático René Descartes (1596-1650) na obra Dioptrique, omitindo o nome de Snellius.

Infelizmente, existem partes da história da Física que estão perdidas ou que são desconhecidas. Por esse motivo, não se sabe a razão de Snellius não publicar sua lei nem o motivo de ela ser publicada por René Descartes nem como os manuscritos de Snellius foram encontrados em um primeiro momento ou como foram perdidos em um segundo momento, muito menos a razão de René Descartes omitir o nome de Snellius. O que se sabe, no entanto, é que existiram esses manuscritos, conferindo a paternidade da lei de Snell a Snellius.

Exercícios resolvidos sobre a lei de Snell

Questão 1

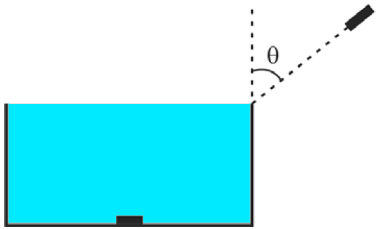
(FMJ) Um raio de luz monocromática se propaga no ar, cujo índice de refração absoluto é igual a 1,0, e incide na superfície de uma lâmina de vidro formando um ângulo com a reta normal à superfície. Ao penetrar no vidro, o raio passa a formar um ângulo com a reta normal.

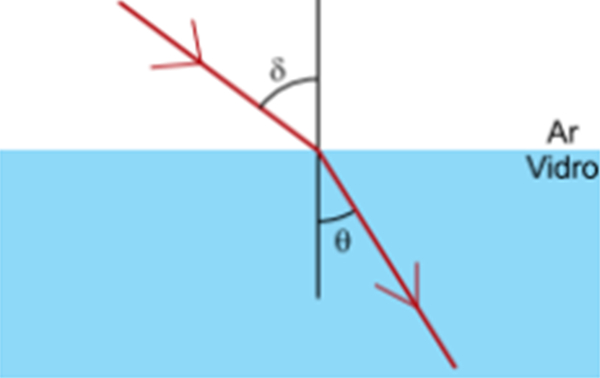
Sabendo que a luz se propaga no ar com velocidade de 3 ∙ 10⁸que \(sen \delta = 0,8 \) e \(sen \theta = 0,6 \)  a velocidade de propagação da luz no vidro que constitui a lâmina é

A) 1,15 ∙ 10⁸ m/s

B) 1,80 ∙ 10⁸ m/s

C) 4,00 ∙ 10⁸ m/s

D) 1,40 ∙ 10⁸ m/s

E) 2,25 ∙ 10⁸ m/s

Resolução:

Alternativa E.

Primeiramente, calcularemos o índice de refração do vidro usando a lei de Snell:

\(n_1 \cdot \sin \theta_i = n_2 \cdot \sin \theta_r \)

\(n_{ar} \cdot \sin \delta = n_{vidro} \cdot sen \theta \)

\(1 \cdot 0,8=n_{vidro} \cdot 0,6\)

\(0,8=n_{vidro} \cdot 0,6\)

\(n_{vidro} = \frac{0,8}{0,6} \)

\(n_{vidro}=1,333\)

Por fim, calcularemos a velocidade da luz no vidro usando a fórmula que o relaciona ao índice de refração do meio e à velocidade da luz no meio:

\(n = \frac{c}{v}\)

\(n_{vidro} = \frac{c}{v} \)

\(1,333 = \frac{3 \cdot 10^8}{v} \)

\(v = \frac{3 \cdot 10^8}{1,333} \)

\(v=225 \ 000 \ 000\)

\(v=2,25 \cdot 10^8 m/s\)

Questão 2

(Unesp) Um semicilindro circular reto de raio R está imerso no ar e é atingido por um raio de luz monocromática que incide perpendicularmente no ponto A de uma de suas faces planas. Após atravessá-lo, esse raio emerge pelo ponto B contido na superfície circular do semicilindro. As figuras indicam as duas situações.

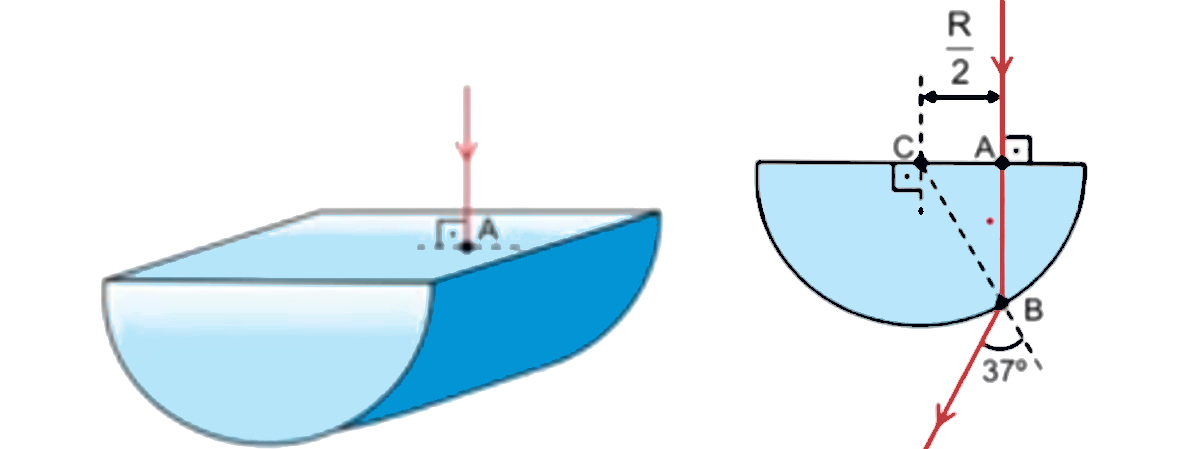
Considerando sen 37° = 0,6 e que o índice de refração absoluto do ar é n_ar = 1 o índice de refração absoluto do material de que o semicilindro é feito é

A) 1,2.   

B) 1,4.   

C) 1,6.   

D) 1,8.   

E) 2,0.

Resolução:

Alternativa A.

Calcularemos o índice de refração absoluto do material de que o semicilindro é feito usando a lei de Snell:

\(n_1 \cdot \sin \theta_i = n_2 \cdot \sin \theta_r\)

\(n_V \cdot \sin \alpha = n_{ar} \cdot \sin 37^\circ \)

\(n_V \cdot \frac{R/2}{R} = 1 \cdot 0,6\)

\(n_V \cdot \frac{R}{2} \cdot \frac{1}{R} = 1 \cdot 0,6 \)

\(n_V \cdot \tfrac{1}{2} = 1 \cdot 0,6 \)

\(n_V=1 \cdot 0,6 \cdot 2\)

\(n_V=1,2\)

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Óptica e Física Moderna (vol. 4). 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: ótica, relatividade e física quântica (vol. 4). 5 ed. São Paulo: Editora Blucher, 2015.